Tetris for Intro/Intermediate Programmers (Summer 2018 update)

Tetris for Intro/Intermediate Programmers (Summer 2018 update)
Step 1: Design Overview

These notes assume that you are familiar with the game of Tetris. If not, we suggest that you first read the Wikipedia entry on Tetris and then play the game a bit. The notes also assume that you are familiar with Python and Tkinter as we have used them in our 15-112 course.

Here is Tetris approximately as we will write it: tetris.jar
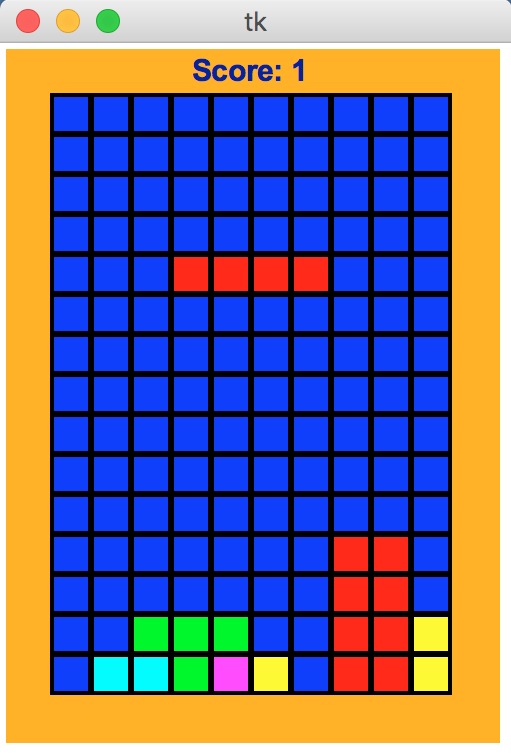
Actually, this is a Java applet/program, and we will write ours in Python, but this can give you a clear idea of our design. As should be clear when you run it, this is a simplified version of Tetris, and many interesting features have been left for you to add as bonus (see Step 8 for details, though also note that bonus points vary by semester). Here is a picture of the game in action:

Our design includes two main elements: a board and a falling piece. In the picture, the board contains all blue (empty) cells except in the bottom three rows, where it contains various other colors. The falling piece is the red piece in the picture. In our design, this is not part of the board, but is drawn over the board.

More specifically, the board is a 2-dimensional list of color names (strings like "red", "blue", "green"). Initially, the board is full of one color, the emptyColor ("blue" in our case). As falling pieces are transferred onto the board, other colors are introduced. The goal of the game is to fill rows entirely with non-empty colors, so that they can then be removed.

The falling piece is a 2-dimensional list of booleans which indicate whether the given cell is or is not painted in this piece. For example, here is the definition of an S piece:

    sPiece = [
        [ False,  True,  True ],
        [  True,  True, False ]
    ]

As noted, the falling piece is not part of the board, but drawn over the board. It becomes part of the board when it can no longer fall and we place it on the board.

General debugging hint: while coding, you almost surely will want to add pausing (say, with "p"), unpausing (also with "p", or maybe "g" for "go"), stepping while pausing (with "s"), and resetting / calling init() again (say with "r"). These can be invaluable when trying to debug animations.

David Kosbie
Carnegie Mellon University
koz@cmu.edu